当前位置:网站首页>GBDT与xgb区别,以及梯度下降法和牛顿法的数学推导
GBDT与xgb区别,以及梯度下降法和牛顿法的数学推导
2020-11-06 01:28:18 【IT界的小小小学生】
为什么要介绍梯度下降法和牛顿法那?
这里提及两个算法模型GBDT和XGBoost,两个都是boosting模型。
GBDT和xgb的目标函数是不同的,同时针对其目标函数中的误差函数 L(θ) 的拟合方式也有差异:
- GBDT利用一阶泰勒展开两项,做一个近似
- xgboost利用二阶泰勒展开三项,做一个近似
言为之意, - GBDT在函数空间中利用梯度下降法进行优化
- XGBoost在函数空间中用牛顿法进行优化
最终的目标函数只依赖于每个数据点的在误差函数上的一阶导数和二阶导数。
针对误差函数可以自定义,比如说平方损失函数: ( y i , y i ) = ( y i − y i ) 2 (yi,y^i) = (yi−y^i)2 (yi,yi)=(yi−yi)2,或logistic损失函数
更多介绍建议去听:https://study.163.com/course/courseMain.htm?courseId=1006401020&share=2&shareId=400000000645014
1. 梯度下降法的推导
梯度下降法在机器学习和深度学习里用的非常多,一般教程或者教材在解释梯度下降法的时候会用形象化的方式(二次曲线、下凸面等),想必大家都知道如何用形象化的方式来说明梯度下降法的有效性。这里,我就不再赘述这种形象化的解释了。我这里使用数学推导来证明梯度下降法的有效性。
一元函数的泰勒展开大家应该都知道,公式如下:
f ( x ) = f ( x 0 ) + f ’ ( x 0 ) 1 ! ( x − x 0 ) + f ’ ’ ( x 0 ) 2 ! ( x − x 0 ) 2 + f ’ ’ ’ ( x 0 ) 3 ! ( x − x 0 ) 3 + … f(x)=f(x_0)+\frac{f’(x_0)}{1!}(x-x_0)+\frac{f’’(x_0)}{2!}(x-x_0)^2+\frac{f’’’(x_0)}{3!}(x-x_0)^3+… f(x)=f(x0)+1!f’(x0)(x−x0)+2!f’’(x0)(x−x0)2+3!f’’’(x0)(x−x0)3+…
不妨只取右边式子的前两项,也就是一个“约等于”的结果:
f ( x ) = f ( x 0 ) + f ’ ( x 0 ) 1 ! ( x − x 0 ) f(x)=f(x_0)+\frac{f’(x_0)}{1!}(x-x_0) f(x)=f(x0)+1!f’(x0)(x−x0)
记: Δ x = x − x 0 \Delta x=x-x_0 Δx=x−x0,上式变为:
f ( x ) = f ( x 0 ) + f ’ ( x 0 ) 1 ! Δ x f(x)=f(x_0)+\frac{f’(x_0)}{1!}\Delta x f(x)=f(x0)+1!f’(x0)Δx
我们的目标是在迭代过程中让下式恒成立,也就是说希望迭代过程中函数值会逐渐减小,用数学语言描述就是: f ( x n + 1 ) ≤ f ( x n ) f(x_{n+1})\leq f(x_{n}) f(xn+1)≤f(xn)
容易想到,应该构造:
Δ x = − f ’ ( x 0 ) \Delta x=-f’(x_0) Δx=−f’(x0)
此时:
f ( x ) = f ( x 0 ) − f ’ ( x 0 ) 2 f(x)=f(x_0)-f’(x_0)^2 f(x)=f(x0)−f’(x0)2
写成迭代形式:
f ( x n + 1 ) = f ( x n ) − f ’ ( x n ) 2 f(x_{n+1})=f(x_{n})-f’(x_{n})^2 f(xn+1)=f(xn)−f’(xn)2
由于 f ’ ( x ) 2 ≥ 0 f’(x)^2\geq 0 f’(x)2≥0,我们就完成了对于梯度下降有效性的证明。从上述步骤归纳出来的参数迭代更新的公式如下:
f ( x n + 1 ) = f ( x n ) − f ’ ( x n ) 2 f(x_{n+1})=f(x_{n})-f’(x_{n})^2 f(xn+1)=f(xn)−f’(xn)2
以上步骤是在一元函数上证明了梯度下降的有效性。容易推广到多元函数。另外,在多元函数中,还可以补充证明梯度方向是下降最快的方向。
详见:知乎为什么梯度下降能找到最小值?
2. 牛顿法
说完了梯度下降法,顺便介绍下牛顿法的推导。因为牛顿法也是通过泰勒展开推导出来的。
继续看泰勒展开:
f ( x ) = f ( x 0 ) + f ’ ( x 0 ) 1 ! ( x − x 0 ) + f ’ ’ ( x 0 ) 2 ! ( x − x 0 ) 2 + f ’ ’ ’ ( x 0 ) 3 ! ( x − x 0 ) 3 + … f(x)=f(x_0)+\frac{f’(x_0)}{1!}(x-x_0)+\frac{f’’(x_0)}{2!}(x-x_0)^2+\frac{f’’’(x_0)}{3!}(x-x_0)^3+… f(x)=f(x0)+1!f’(x0)(x−x0)+2!f’’(x0)(x−x0)2+3!f’’’(x0)(x−x0)3+…
依旧,我们取右式的前2项:
f ( x ) = f ( x 0 ) + f ’ ( x 0 ) 1 ! ( x − x 0 ) f(x)=f(x_0)+\frac{f’(x_0)}{1!}(x-x_0) f(x)=f(x0)+1!f’(x0)(x−x0)
对等式两边取导数:
f ’ ( x ) = f ’ ( x 0 ) + f ’ ’ ( x 0 ) 1 ! ( x − x 0 ) f’(x)=f’(x_0)+\frac{f’’(x_0)}{1!}(x-x_0) f’(x)=f’(x0)+1!f’’(x0)(x−x0)
f ’ ( x ) = f ’ ( x 0 ) + f ’ ’ ( x 0 ) 1 ! Δ x f’(x)=f’(x_0)+\frac{f’’(x_0)}{1!}\Delta x f’(x)=f’(x0)+1!f’’(x0)Δx
根据微积分的性质, f ( x ) f(x) f(x)取最小值时,有 f ’ ( x ) = 0 f’(x)=0 f’(x)=0,我们把这个性质代入上面的式子,有:
0 = f ’ ( x 0 ) + f ’ ’ ( x 0 ) 1 ! Δ x 0=f’(x_0)+\frac{f’’(x_0)}{1!}\Delta x 0=f’(x0)+1!f’’(x0)Δx
Δ x = − f ’ ( x 0 ) f ’ ’ ( x 0 ) \Delta x=-\frac{f’(x_0)}{f’’(x_0)} Δx=−f’’(x0)f’(x0)
这样我们就得到了牛顿法的参数迭代更新公式如下:
x n + 1 = x n − f ’ ( x n ) f ’ ’ ( x n ) x_{n+1}=x_{n}-\frac{f’(x_n)}{f’’(x_n)} xn+1=xn−f’’(xn)f’(xn)
3. 梯度下降法和牛顿法的异同
从上面的证明过程可以看出,梯度下降法和牛顿法虽然都可以用泰勒展开推导,但推导所依据的思想还是有一点不一样的。
在实际运用中,牛顿法和梯度下降法都是广泛应用于机器学习中的。两者的区别其实很多博客都有写,比如:梯度下降or拟牛顿法?
4. 拟牛顿法
在上面牛顿法的参数迭代更新公式中,我们可以看到 f ’ ’ ( x 0 ) f’’(x_0) f’’(x0)是位于分母部分的。记住,上面的数学推导是用的一元函数,对于多元函数,这个分母存在相当于要计算Hessian矩阵的逆矩阵,这是非常困难且耗费时间的。因此,很多牛顿算法的变形出现了,这类变形统称拟牛顿算法。BFGS是用迭代法去近似计算海森矩阵。而BFGS需要额外储存近似的那个海森矩阵,所以有了改进版L-BFGS。
版权声明
本文为[IT界的小小小学生]所创,转载请带上原文链接,感谢
https://vip01.blog.csdn.net/article/details/85855497
边栏推荐
- C++ 数字、string和char*的转换
- C++学习——centos7上部署C++开发环境
- C++学习——一步步学会写Makefile
- C++学习——临时对象的产生与优化
- C++学习——对象的引用的用法
- C++编程经验(6):使用C++风格的类型转换
- Won the CKA + CKS certificate with the highest gold content in kubernetes in 31 days!
- C + + number, string and char * conversion
- C + + Learning -- capacity() and resize() in C + +
- C + + Learning -- about code performance optimization
猜你喜欢
-
C + + programming experience (6): using C + + style type conversion
-

Latest party and government work report ppt - Park ppt
-
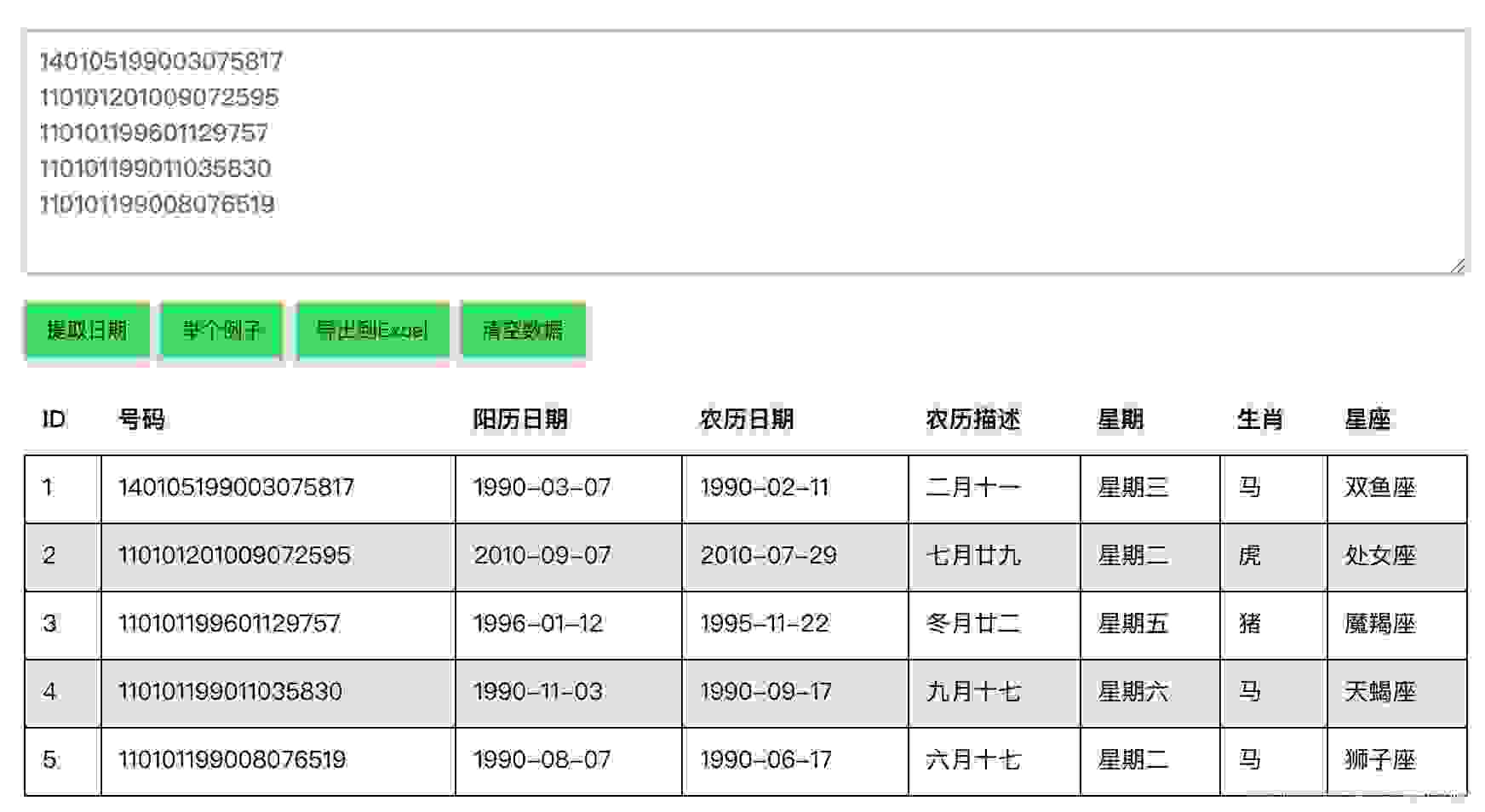
在线身份证号码提取生日工具
-

Online ID number extraction birthday tool
-
️野指针?悬空指针?️ 一文带你搞懂!
-
Field pointer? Dangling pointer? This article will help you understand!
-
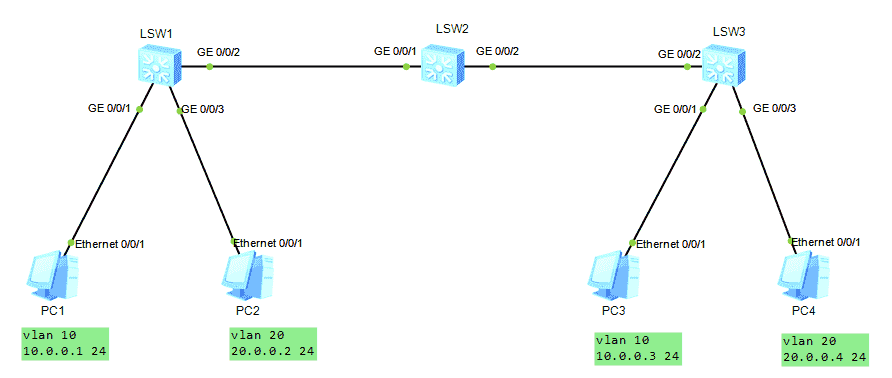
HCNA Routing&Switching之GVRP
-

GVRP of hcna Routing & Switching
-

Seq2Seq实现闲聊机器人
-
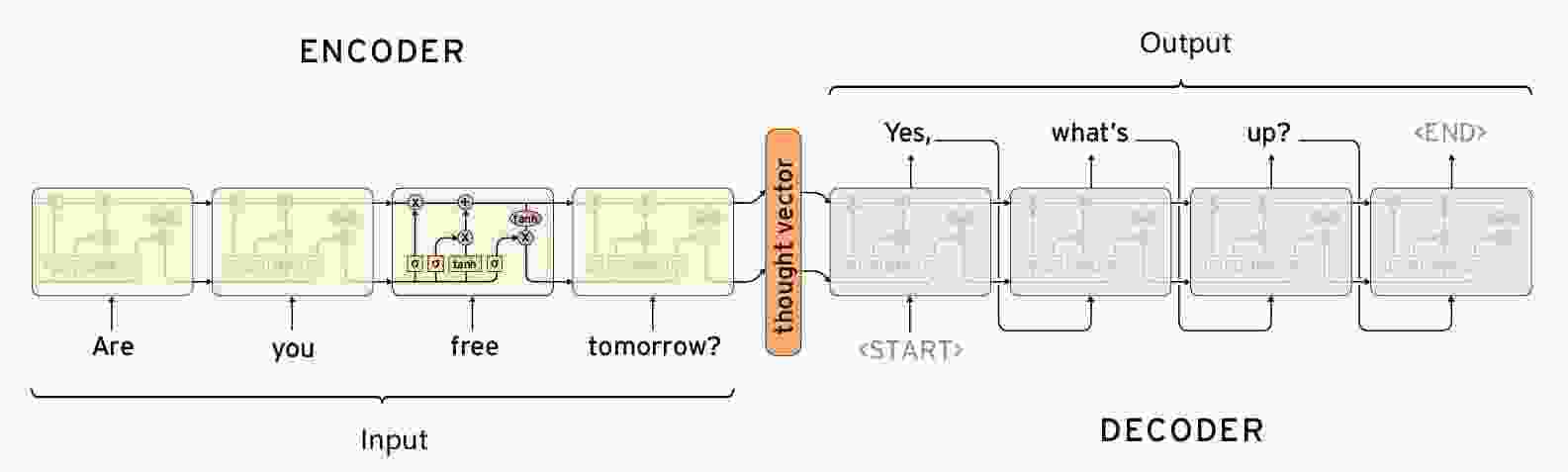
【闲聊机器人】seq2seq模型的原理
随机推荐
- LeetCode 91. 解码方法
- Seq2seq implements chat robot
- [chat robot] principle of seq2seq model
- Leetcode 91. Decoding method
- HCNA Routing&Switching之GVRP
- GVRP of hcna Routing & Switching
- HDU7016 Random Walk 2
- [Code+#1]Yazid 的新生舞会
- CF1548C The Three Little Pigs
- HDU7033 Typing Contest
- HDU7016 Random Walk 2
- [code + 1] Yazid's freshman ball
- CF1548C The Three Little Pigs
- HDU7033 Typing Contest
- Qt Creator 自动补齐变慢的解决
- HALCON 20.11:如何处理标定助手品质问题
- HALCON 20.11:标定助手使用注意事项
- Solution of QT creator's automatic replenishment slowing down
- Halcon 20.11: how to deal with the quality problem of calibration assistant
- Halcon 20.11: precautions for use of calibration assistant
- “十大科学技术问题”揭晓!|青年科学家50²论坛
- "Top ten scientific and technological issues" announced| Young scientists 50 ² forum
- 求反转链表
- Reverse linked list
- js的数据类型
- JS data type
- 记一次文件读写遇到的bug
- Remember the bug encountered in reading and writing a file
- 单例模式
- Singleton mode
- 在这个 N 多编程语言争霸的世界,C++ 究竟还有没有未来?
- In this world of N programming languages, is there a future for C + +?
- es6模板字符
- js Promise
- js 数组方法 回顾
- ES6 template characters
- js Promise
- JS array method review
- 【Golang】️走进 Go 语言️ 第一课 Hello World
- [golang] go into go language lesson 1 Hello World