当前位置:网站首页>二叉树的常见算法总结
二叉树的常见算法总结
2020-11-06 01:18:19 【ClawHub的博客】
节点定义
1 |
public static class BinaryNode<T> { |
二叉树节点包括元素值与左右子节点引用。
创建节点
1 |
BinaryNode g = new BinaryNode(7); |
形如:
1、前、中、后序遍历
二叉树的前、中、后序遍历中的前、中、后指的是根节点;
前序:先输出根节点,之后左右节点。
中序:先左,之后输出根节点,再右。
后序:先左右,再输出根节点。
1 |
public static void visit(BinaryNode p) { |
1.1、前序遍历
1 |
根->左->右 |
1.1.1、递归实现
1 |
public static void recursivePreOrder(BinaryNode p) { |
如果节点为null,直接返回;
先打印出根节点,之后递归左子树,再递归右子树。
正好符合:先根,再左右。
1.1.2、非递归实现
1 |
public static void iterativePreOrder(BinaryNode p) { |
充分利用了栈的思路,先进后出。
当节点非空时,将节点入栈,迭代栈内元素,弹出栈顶元素,当前为根元素,之后将其右左子节点分别压栈。这样子节点出栈的顺序就是先左再右。
1.2、中序遍历
1 |
左->根->右 |
1.2.1、递归实现
1 |
public static void recursiveInOrder(BinaryNode p) { |
1.2.2、非递归实现
1 |
public static void iterativeInOrder(BinaryNode p) { |
1.3、后序遍历
1 |
左->右->根 |
1.3.1、递归实现
1 |
public static void recursivePostOrder(BinaryNode p) { |
1.3.2、非递归实现
1 |
public static void iterativePostOrder(BinaryNode p) { |
2、BFS与DFS
2.1、BFS广度优先搜索
1 |
1234567 |
广度优先遍历就是按层读取节点元素,需要借助队列的数据结构。
1 |
public static void levelOrderTraversal(BinaryNode node) { |
2.2、DFS深度优先搜索
1 |
1245367 |
从根节点出发,选择一条分支读取所有的元素,需要借助栈的数据结构。
1 |
public static void depthTraversal(BinaryNode node) { |
3、二叉树的深度
3.1、递归
1 |
private static int calcDepth(BinaryNode node) { |
3.2、深度优先
maxDepth与每个分支的长度做比较更新,最终获取最深的分支长度。
1 |
public static int maxDepthDFS(BinaryNode node) { |
3.3、广度优先
按层搜索,每进入一层,深度+1.
1 |
public static int maxDepthBFS(BinaryNode node) { |
4、二叉树镜像
通过深度或者广度遍历,将节点的左右子树交换。
1 |
public static void mirror(BinaryNode root) { |
5、对称二叉树
101. 对称二叉树
这道题就是二叉树镜像的变种,如果两个二叉树对称,则:
- 两个根节点具有相同的值
- 每个树的左子树,都与另一个树的右子树相同
递归实现:迭代实现:1
2
3
4
5
6
7
8
9
10
11public boolean isSymmetric(BinaryNode root) {
return isMirror(root, root);
}
public boolean isMirror(BinaryNode t1, BinaryNode t2) {
if (t1 == null && t2 == null) return true;
if (t1 == null || t2 == null) return false;
return (t1.val == t2.val)
&& isMirror(t1.right, t2.left)
&& isMirror(t1.left, t2.right);
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17public boolean isSymmetric(BinaryNode root) {
LinkedList<BinaryNode> q = new LinkedList<>();
q.add(root);
q.add(root);
while (!q.isEmpty()) {
BinaryNode t1 = q.poll();
BinaryNode t2 = q.poll();
if (t1 == null && t2 == null) continue;
if (t1 == null || t2 == null) return false;
if (t1.val != t2.val) return false;
q.add(t1.left);
q.add(t2.right);
q.add(t1.right);
q.add(t2.left);
}
return true;
}
总结
二叉树的各种题目的算法在第一意识里会想到递归,但是递归深度过大时会出现栈溢出,所以相应的会使用迭代来实现,相应的也就引入队列或者栈的数据结构。
感觉最重要的算法就是DFS与BFS,其中DFS深度优先搜索使用栈的先进后出特性,而BFS广度优先搜索则使用队列的先进先出特性。
版权声明
本文为[ClawHub的博客]所创,转载请带上原文链接,感谢
https://clawhub.club/posts/2020/01/02/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E4%B8%8E%E7%AE%97%E6%B3%95/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E5%B8%B8%E8%A7%81%E7%AE%97%E6%B3%95%E6%80%BB%E7%BB%93/
边栏推荐
- C++ 数字、string和char*的转换
- C++学习——centos7上部署C++开发环境
- C++学习——一步步学会写Makefile
- C++学习——临时对象的产生与优化
- C++学习——对象的引用的用法
- C++编程经验(6):使用C++风格的类型转换
- Won the CKA + CKS certificate with the highest gold content in kubernetes in 31 days!
- C + + number, string and char * conversion
- C + + Learning -- capacity() and resize() in C + +
- C + + Learning -- about code performance optimization
猜你喜欢
-
C + + programming experience (6): using C + + style type conversion
-

Latest party and government work report ppt - Park ppt
-
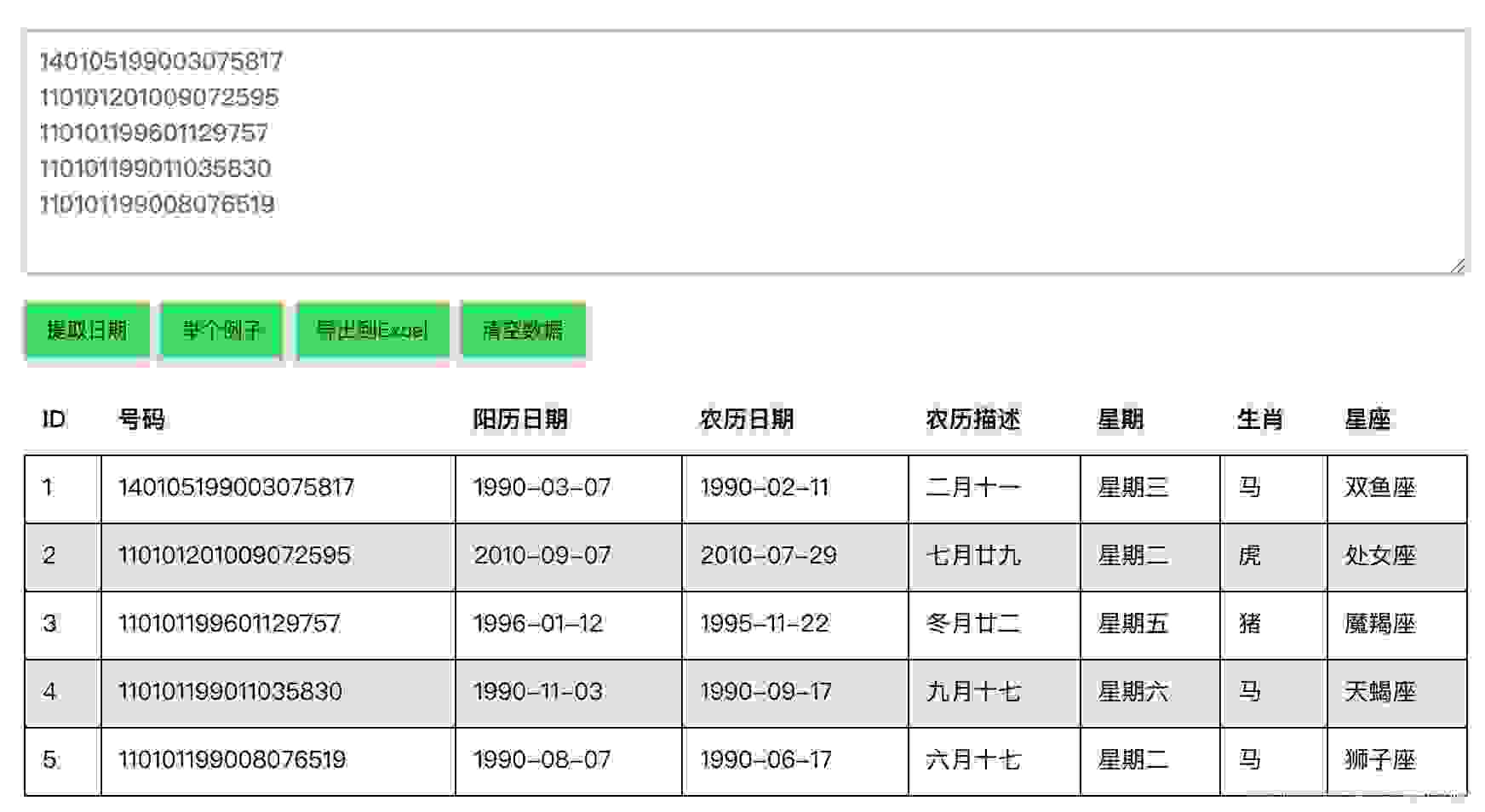
在线身份证号码提取生日工具
-

Online ID number extraction birthday tool
-
️野指针?悬空指针?️ 一文带你搞懂!
-
Field pointer? Dangling pointer? This article will help you understand!
-
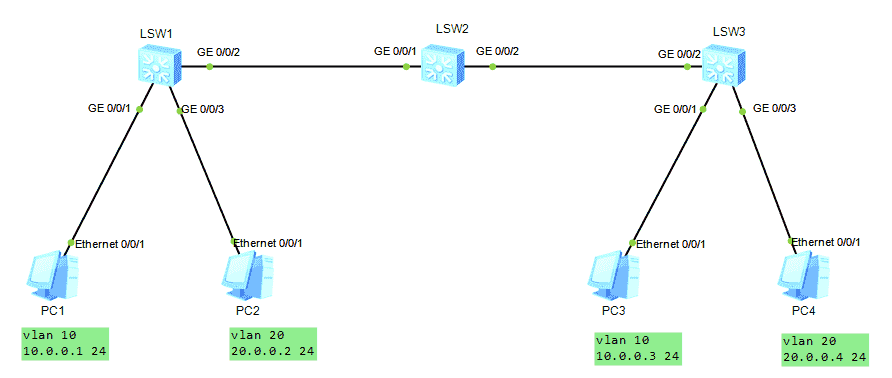
HCNA Routing&Switching之GVRP
-

GVRP of hcna Routing & Switching
-

Seq2Seq实现闲聊机器人
-
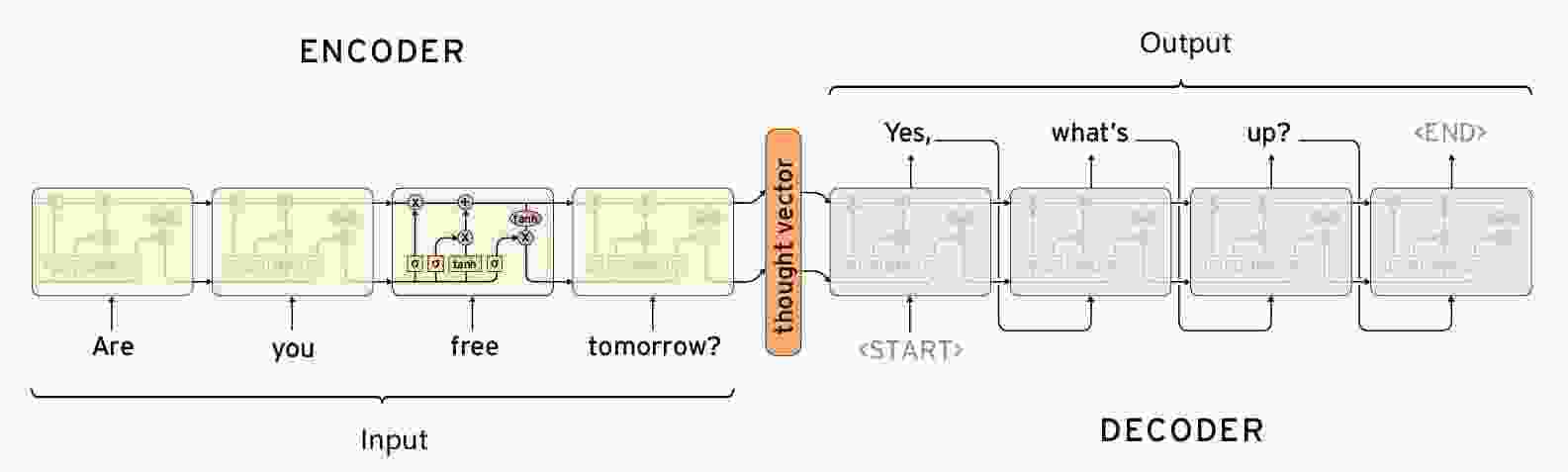
【闲聊机器人】seq2seq模型的原理
随机推荐
- LeetCode 91. 解码方法
- Seq2seq implements chat robot
- [chat robot] principle of seq2seq model
- Leetcode 91. Decoding method
- HCNA Routing&Switching之GVRP
- GVRP of hcna Routing & Switching
- HDU7016 Random Walk 2
- [Code+#1]Yazid 的新生舞会
- CF1548C The Three Little Pigs
- HDU7033 Typing Contest
- HDU7016 Random Walk 2
- [code + 1] Yazid's freshman ball
- CF1548C The Three Little Pigs
- HDU7033 Typing Contest
- Qt Creator 自动补齐变慢的解决
- HALCON 20.11:如何处理标定助手品质问题
- HALCON 20.11:标定助手使用注意事项
- Solution of QT creator's automatic replenishment slowing down
- Halcon 20.11: how to deal with the quality problem of calibration assistant
- Halcon 20.11: precautions for use of calibration assistant
- “十大科学技术问题”揭晓!|青年科学家50²论坛
- "Top ten scientific and technological issues" announced| Young scientists 50 ² forum
- 求反转链表
- Reverse linked list
- js的数据类型
- JS data type
- 记一次文件读写遇到的bug
- Remember the bug encountered in reading and writing a file
- 单例模式
- Singleton mode
- 在这个 N 多编程语言争霸的世界,C++ 究竟还有没有未来?
- In this world of N programming languages, is there a future for C + +?
- es6模板字符
- js Promise
- js 数组方法 回顾
- ES6 template characters
- js Promise
- JS array method review
- 【Golang】️走进 Go 语言️ 第一课 Hello World
- [golang] go into go language lesson 1 Hello World